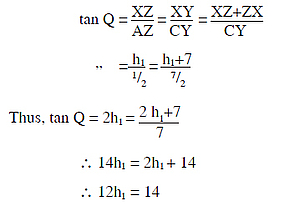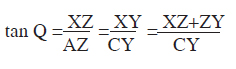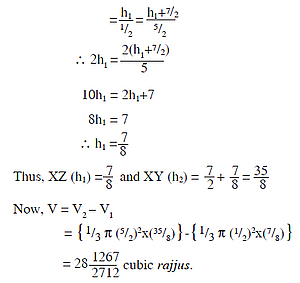Let us examine the above calculation made by the Dhavalākāra in the light of modern mathematical method. In order to find out the value of the adholoka (in mṛdañgākāra loka) we know that it is in the shape of a chopped off right conical pyramid. (See figure no. 2).

When we extend the hypotaneouses of the triangles to meet at an apex, we get the figure of the complete pyramid. (See figure no. 3)

We know that distances:
ZY = 7 rajjus = h
CD = 7 rajjus = d2
CY = 7/2 rajjus = r2
AB = 1 rajju = d1
AZ = 1/2 rajju = r1
We have to find out the volume of the whole pyramid XCD
and also the small pyramid XAB. Then we get the volume of adholoka as -
= Volume of Pyramid XCD - Volume of Pyramid XAB
First we have to calculate the height XZ, say h1.
Let Q denote the ∠XAZ, which is equal to ∠XCY. Then
∴ h1 = 14/12 = 7/6
Thus, XZ = 7/6 rajjus and XY = 7 + 7/6 rajjus = 49/6 rajjusVolume of a right conical pyramid is given by
V = 1/3 πr2h
Thus, volume of pyramid XAB
V1 = 1/3 π(½)2 x (7/6)
Taking the value of π as 355/113, we get
By comprising this value with the value of the volume of adholoka given by Vīrasenācārya, which is 106 261/1356 cubic rajjus, we find that the latter is not exact. This is for two reasons:
(1) The value of π taken is 371/113 (= 3.28...... approximately) instead of actual value of π taken by us which is 355/113 (= 3.14......approximately).
If we also take
π = 371/113
We will get
V = 109 335/4068
In the same way, we can also find out the volume of ūrdhvaloka.
The ūrdhvaloka can be divided into two equal halves.

In the upper half (see fig. 4), the distance XZ (h1) can be found as before thus:
∴ The total volume of ūrdhvaloka 2 x V = 56 1267/1356 cubic rajjus. Here, also the difference in the volume found by Vīrasenācārya and that found through modern mathematical method is worth noting.
 Prof. Muni Mahendra Kumar
Prof. Muni Mahendra Kumar