The second method is based on the expression that the distance between the two vedikās, situated diametrically opposite to each other, on the savyambhuraman ocean, which is the last of the concentric rings of continents and oceans, is called one rajju.[1] It is believed that there are innumerable number of continents and oceans, in the form of concentric circles. (See fig.15)
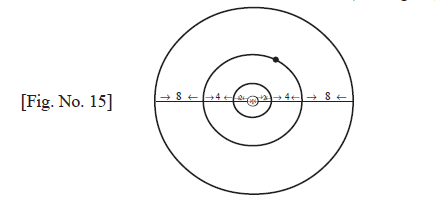
The diameter of the first circle which is a continent known as Jambūdvīpa is exactly 1,00,000 yojanas, where 1 yojana is measured by pramaṇa-aṅgula which is 1000 times utsedha-aṅgula (for the relation between aṅgula and yojanas see appendix I). The second ring is an ocean which has the diameter (here the diameter means the thickness of the ring) of 2x105 yojanas. The third ring is again a continent which has the diameter of 4x105 yojanas, and so on. Thus, the diameters of all the rings are in geometric progression with common ratio of 2x105 yojanas. Then, the actual diameter (not the thickness) of the last circle (which is the ocean called svayambhūramaṇa), is equal to twice the sum of the diameters (thickness) of all the rings minus the diameter of the first ring (because all the other rings will be encountered twice, while the first circle will be encountered only once). This is equal to 1 rajju. Symbolically writing 1 rajju.
= 2 x Σ diameters of the all rings minus the diameter of the first ring.
The diameter of the first ring is equal to 105 yojanas. If n is the number of all rings, then Σ diameters of all rings.
= {(2n-1)x105} yojanas.
1 rajju
= {2 [(2n-1)x105]-(10-5)} yojanas
= {2n+1-3)x105} yojanas.
The number n is not given, But it can be calculated from the expression that, the no. of all continents and oceans is equal to the number of "samayas" in 2.5 sukṣma -uddhāra-sāgaropama, which is equal to 25 koṭākoṭi sukṣma-uddhāra-palyopamas (S.U.P.)[2] 61-9.
Palyopama and Sāgaropama are time-units.[3] One koṭākoṭi =1014.
Now, to calculate the exact number of "samayas" in one S.U.P. is not possible. But again here we can find the lowest possible value of this number. The value of the number of samayas in one S.U.P. is[4]
= 3.3 x 1036 x asaṃkhyāta.
Here again, we substitute the number 'Śīrṣaprahelikā' in the place of asaṃkhyāta. Then, number of samayas in one S.U.P.
= 3.3 x 1036 x (7.58x10193)
= 2.5x10230
Then, the number of samayas in 25 koṭākoṭi S.U.P. which is equal to n) is
n = (25 x 1014) x (3.3 x 1036) x 7.58 x 10193
= 6.25 x 10245
Substituting the value of n in the expression for rajju, we get,
1 rajju = {2[(6.25 x 10245)+1]-3}x 105 yojanas
= 10(1.88 x 10245) yojanas approximately.
Taking 1 yojana = 8000 miles,
1 rajju = 8.0 x 10{(1.88 x 10245)+3} miles.
Expressed in terms of light-years,
4.704 x 10{(1.88 x 10245)-9} light years
The volume (which is 343 cubic rajjus) will be - (in terms of cubic miles) -
17.6 x 10{(5.64 x 10245) +13} cubic miles
The volume (in terms of cubic light-years) will be-
3.56 x 10{(5.64 x 10245) -23} cubic light years
Alternatively, if we take 1 yojana = 4000 miles, according to the Digambara tradition, then
The value of 1 rajju (in terms of miles) will be
1 rajju = 4.00 x 10{(1.8 x 10245) +3} miles
The value of 1 rajju (in terms of light-years) will be-
2.352 x 10{(1.88 x 10245) -9} light years
The value of the volume (in terms of cubic miles) will be-
22 x 10{(5.64 x 10245) +13} cubic miles
The value of the volume (in terms of cubic light-years) will be-
0.445 x 10{(5.64 x 10245)-23} cubic light years
Thus, we have found the values of rajju and the volume of loka on the basis of two different methods. We should keep in mind that actual values will be much more than these, which can be estimated on the basis of the magnitude of J.P.A.[5]
We may summarise the above mathematical discussion thus:
- The universe has a definite shape called supratiṣṭhaka.
- The volume of the universe, in no case, is less than cubic miles
pramaṇa āṅgulaniṣpannayojanānāṃ pramāṅataḥ.
asaṃkhyakoţākoţ ibhirekā rajjuḥ prakīrtitā..
svayambhūramaṇābdherye pūrvapaścimavedike.
tayoḥ parāntāntarālaṃ rajjumānamidaṃ bhavet.. - Lokaprakāśa, 1.64-65.
 Prof. Muni Mahendra Kumar
Prof. Muni Mahendra Kumar

