The Enigma Of The Universe : Mathematical Computation

Let us use the same notations which we had used in the previous calculation

Radius r_o = (12288 x 10¹¹) sarṣapas Height h = (24784.896 x 10⁹) sarṣapas

Now, k_o^th seed will be dropped in cylinder A, and it will be completely filled. Then the first seed will be dropped in the cylinder B. Again one by one, the seeds from the cylinder A will be dropped in the rings ahead. The last seed will be dropped in the

Now, by dropping the ko seeds in the cylinder A, it will be filled completely. Then the second seed will be dropped in the cylinder B. By dropping one by one the seeds of the cylinder A in the rings ahead, its last seed will be dropped in the

Now, by repeating the same process, when the cylinder X_{ko 2} will be emptied, one seed will be dropped in the cylinder A and it will be completely filled k_o^th time. Then one seed will be dropped in the cylinder B and it will also be completely filled for the first time, and the first seed will be dropped in the cylinder C, since the last seed of X_ko

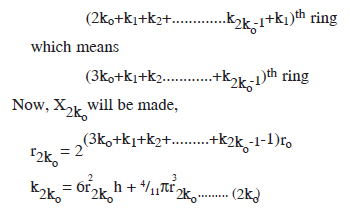
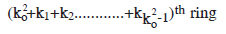
Now, by emptying the cylinder B, its last seed will be dropped in the

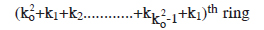
Now, the cylinder A also will be emptied. Its last seed will be dropped in the

Now, at this moment, by dropping one seed in the cylinder A, it will be completely filled, and consequently one seed will be dropped in the cylinder B and it will be also completely filled. As a result, one seed will be dropped in the cylinder C and that too will be completely filled. Ultimately the new anavasthita kuṇḍa

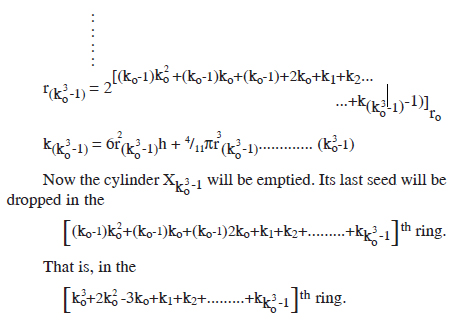
Although the number in the { } is quite small in comparison to 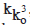, it definitely makes a valuable contribution in making the value of U. S. quite great. Now, we can see that the equations no. (0) to (k_o ³) define precisely the value of 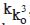, yet it is not possible to evaluate it through simple mathematical operations.

It should also be noted that the value of 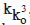3 obtained in the Shvetambara tradition is greater than that obtained in the Digambara tradition.