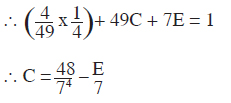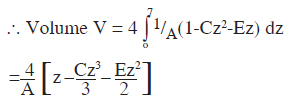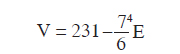We have already discussed how in the Shvetambara tradition, the volume of the loka is believed to be 343 cubic rajjus, but the exact shape is to be determined so that all the fundamental beliefs are kept intact.
We consider first the adholoka.
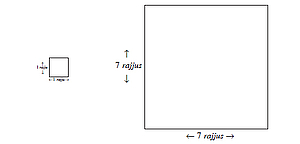
We know that it is fundamentally accepted that both dimensions- length and breadth-at any height of the loka should be equal. Again, at the bottom they are 7 rajjus and at the top (of the adholoka) they are 1 rajju. The total height of the adholoka is 7 rajjus.
Now, there are two possible shapes of the plane with equal length and breadth:
1. It is a circle.
2. It is a square
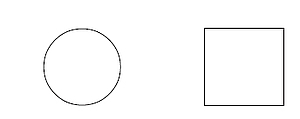
As we have seen, in mṛdañgākāra loka, it is believed to be a circle, whereas in the method used to find out vargita khaṇḍukas (see supra, p....) it is believed to be a square. Here, we select the letter possibility and find out the shape of the adholoka. It means that at any point, the horizontal cross section of the loka is a square. At the top the adholoka is a square of 1 rajju length and breadth and at the bottom it is a square of 7 rajjus dimensions.
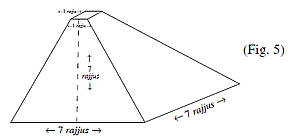
Now, in the adholoka as we move from top to bottom, there is a gradual increase in the dimensions, and hence, the squares at any plane become larger and larger up to the bottom. Starting from 1 rajju in length and breadth, they gradually become 7 rajjus in length and breadth. We do not have the information about the size of the intermediate squares and also about the shape of the line joining the squares. It is obvious that if it is assumed to be straight (see fig. 5) we do not get the required volume which is 196 cubic rajjus.
Let us assume that it is curved. Now we use integral calculus to determine the exact shape of the universe.
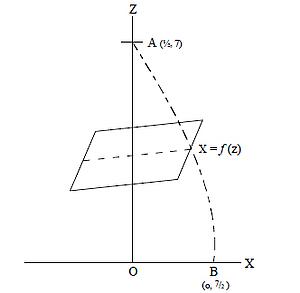
Let ox, oz represent the axes. AB is the curve joining the corresponding points on the squares. Let x=f(z) be the equation of such a curve. Then the volume of the solid figure bounded by such curves and squares is given by
V = 4 ∫ x2dz
between proper limits. Out of the infinite number of curves passing through A, B, we have to find out the required curve. One of the possibilities is that it is a conic. Let the conic be represented by the equation-
Ax2+Bxz+Cz2+Dx+Ez = 1
Then, because the curve is symmetrical about the z axis, the co-efficient B & D will be equal to zero. Thus, the equation of conic is-
Ax2+Cz2+Ez = 1
 x2 = 1/A (1-Cz2-Ez)
x2 = 1/A (1-Cz2-Ez)
The points (7/2, 0, 0) & (1/2, 0, 7) lie on the curve.
when x = 7/2, z = 0 i.e. A = 4/49
Also when x = 1/2, z = 7
The integration is from z1=0 to z2=7
Putting the values of A and C we get,
Thus the value of V depeneds upon E; for different E, the volumes can have different values. The volume of adholoka is 196. From the above equation, we see that
If E = 30/73, V = 196
Thus we have found the equation of the curve, which passes through the corresponding points on the squares. The equation is given by-
196X2+18Z2+210Z = 2401
In the same way we can find the equation of the curves making the ūrdhvaloka. The ūrdhvaloka should be divided into two equal halves, each having the volume 147/2.
Then we have the equation-
196X2+192Z2-1008Z = 49
and 196X2+192Z2-336Z = 1225
Representing the lower and upper halves of the ūrdhvaloka respectively.
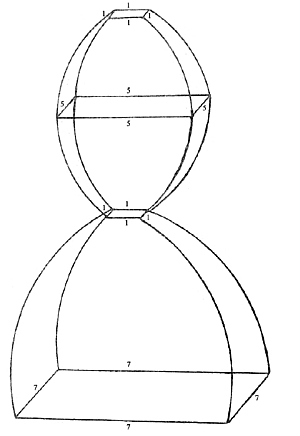
Thus, the shape given by the equations given above, furnishes us with the exact shape of the universe which has the volume of 343 cubic rajjus.
 Prof. Muni Mahendra Kumar
Prof. Muni Mahendra Kumar