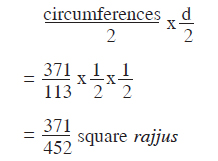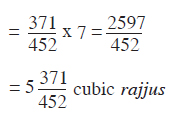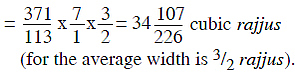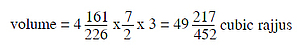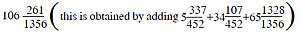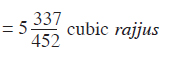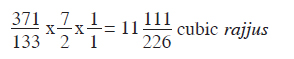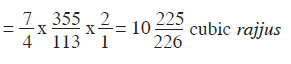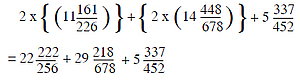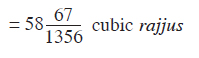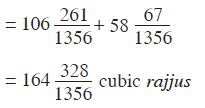Acharya Virasena has found out the volume of Loka which has the shape of mṙdaṅga (tabor), in his commentary Dhavalā on Ṣaţkhaṇḍāgama.[1] The whole discussion is given here in toto:
"Firstly, let the central portion of the loka which is 14 rajjus in height, having a circular base and a diameter of 1 rajju be considered separately. (See figure 1). Now the method of determine its volume is:
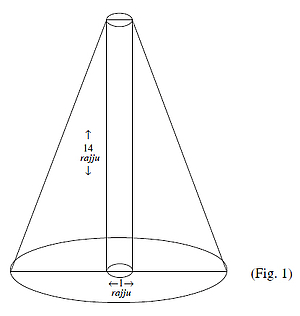
[Here there value of π is taken as 371/113. Actually it should have been 345/113 (see Appendix II, fn. 3 on p. 346)] This cylinder (sucī) has the width of only one space-unit. The circumference of its circular base which has a diameter of 1 rajju is 371/113 rajjus. (This is π rajjus, for the diameter is 1 rajju). The area is given by
The volume of the right circular cylinder with height 7 rajjus is given by
area x height
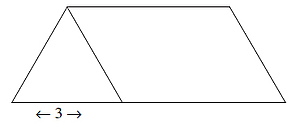
Now the lower universe from which the above cylinder is taken out is made to take a shape of sūrpa, i.e., winnowing-basket (by spreading it), which at the top has the dimension of 371/113 and at the base the dimension of 22 15/13 rajjus. Now by cutting this figure downwards up to 7 rajjus (which is the height) into three parts, we get two triangles and one rectangle, which is in the middle (see figure II).
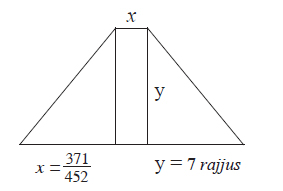
The middle rectangular portion has also the height of 7 rajjus and the dimension of the base is 371/113 rajjus. Now the width of this rectangular solid is 1 space-unit at the top and 3 rajjus at the bottom; therefore the volume is given by
height x length at the top x width
Now there are two triangular figures which are 7 rajjus in length, and has the bhujā (base) of 9 48/113 rajjus. This is called bhujā of the triangle. But it is actually the karṇa (hypotaneous) of both triangles. Now, the triangle is divided into three parts by dissecting the hypotaneous into three equal parts.
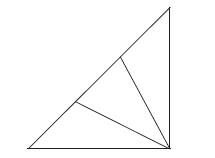
Now, in each of these three portions, there are two triangles and one rectangle. Now, the height of each rectangle on both sides of the seven rajjus high rectangle is 7/2 rajjus and width is 4161/226 rajjus, while the width at both lowermost corners on right and left is 3 rajjus. The width at the right and left corners is 3/2 rajjus. Now by putting together both the rectangular portions one above other, we get a rectangular solid with the same width on all sides equal to 3 rajjus. Now by multiplying the length with the height and again by multiplying with the width, the volume is obtained. Thus,
Now, the remaining four triangular regions are considered. Each has the height 7/2 rajjus, and bhujā equal to 4 161/226 rajjus.
Now, joining them together on the hypotaneous sides, and cutting them on both sides in the middle, we get four rectangles and eight triangles.
Now, the volume of the four rectangular-based portions is ¼ of the volume of the former rectangular portions, because by joining all the four portions with the same width, that is by putting them upside down in opposite ways, we get the region with 3 rajjus width and rest dimensions equal to half of the dimensions of former reatangles.
Now, the remaining eight triangular-based portions are again re-arranged as before so as to form 16 triangles and 8 rectangles.
Now, by taking the half dimensions of former rectangles, the volume of the each of the eight rectangular portion will be ¼ of the volume of the four rectangular regions mentioned now. Now, in the same way, dissecting further the remaining portions each time into 16, 32, 64...... rectangular-based portions, the volume of each rectangular-based portion every time obtained will be ¼ of the former ones, up to...... the dimension equal to single space unit. By adding the volume of all rectangular-based portions we get the value say x, of the volume of that part of adholoka, which when added to the former values found, make the total volume of adholoka. The value x is obtained by multiplying the area of the last rectangle in the previous operation by 4, and then divide it by (4-1=) 3, thus,
Then by adding all the parts we get the total volume of the adholoka which is
In the same way, we can find the volume of the ūrdhvaloka. Firstly, the volume of the central cylindrical portion is (as before)
Then, we find the volume of the half of the ūrdhvaloka (upper universe) in the same way as the volume of adholoka was found.
Then, the remaining part of ūrdhvaloka is converted into the shape of sūrpa. Its dimensions at the top and bottom are 371/113 and 1596/113 rajjus respectively. The width at the top is only one space unit, and the width at the middle is 2 rajjus and at the other end it becomes again only 1 space-unit. Then, as before, the sūrpa-shaped region is dissected to form two triangles and one rectangle. First, we find the volume of the rectangular-based portion which has the dimensions of 7/2 rajjus height, 332/113 rajjus wide, 2 rajjus wide at bottom and one space-unit wide at the top. By multiplying the height (7/2 rajjus) with the viṣkambha (371/113 rajjus) and again multiplying it with the width (1 rajju), we get the volume of this portion as:
Again, as before, the two triangles which are 7/2 rajjus in height and 632/113 rajjus wide, are divided in the middle to form 4 triangles and 2 rectangles which have 7/4 rajjus height and 3 16/113 rajjus width and are 2, 1, and 1 rajju thick respectively are considered (as before): By placing one rectangle above the other, we get the region of 2 rajjus width. Then by multiplying the viṣkambha 355/113 rajjus) with the utṣedha (7/4 rajjus) (utṣedha is height) and again multiplying it with the width (2/1 rajjus), we get the volume
The volume of the remaining 4 triangular-based portions is ¼ the volume of the rectangular-based portion. As said, before, the total volume of all triangles is (1/4 x10 225/226) cubic rajjus.
This, when added to 10 225/226 cubic rajjus, we get 14 448/678 cubic rajjus.
Total volume of both the parts of the ūrdhvaloka is given by
Now by adding the volumes of adholoka and ūrdhvaloka, we get the total volume of loka, which is
But the ghanaloka is
= 73 = 343 cubic rajjus
Thus, the volume of mṛdañgākāra loka, as believed by other ācāryas is only a numerical fraction of the ghanaloka but there is no loka different from the ghanaloka which is actually the container of six dravyas and which is of volume equal to cube of 7 rajjus standing in the alokākāśa. Therefore, the belief of mṛdañgākāra loka is not acceptable."
 Prof. Muni Mahendra Kumar
Prof. Muni Mahendra Kumar