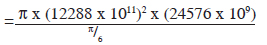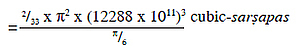On the basis of the above definition of the U.S., we can make its exact mathematical computation as follows:
The first thing to be calculated is the number of seeds which are filled in Xo. This number can be calculated if we know-
1. The dimensions of a single mustard (sarṣapa) seed.
2. The number of such mustard seeds contained in the right circular cylinder of diameter 1,00,00 yojanas and height 1000 yojanas.
3. The number of seeds contained in the conical heap.
Now, we proceed to calculate these three numbers. We find that sarṣapa is the name of a linear measure which is equal to the diameter of one mustard seed (which is also called sarṣapa) and which has a perfectly spherical shape. According to one tradition found in the Trilokasāra,[1] we get
8 sarṣapas = 1 yava
8 yavas = 1 aṅgula.
1 aṅgula = 64 sarṣapas
Now, as we have already seen the diameters of the continents of oceans are measured by 'paramāṇāngula'; we get, therefore, from the table of space-points (see supra p. 334-336).
1 yojana = (768000 x 500) utṣedha- aṅgula
1 yojana = (768000 x 500 x 64) sarṣapas
= 24576000000 sarṣapas
radius of the circular base of the cylinder
= 50000 yojanas
= 12288 x 1011 sarṣapas
and height of the cylinder = 1000 yojanas= 24576 x 109 sarṣapas
volume of 1 seed of sarṣapa = 4/3 π (radius)3radius of the seed of sarṣapa = ½ sarṣapa;
... volume of one seed of sarṣapa= 4/3 π (½)3 cubic sarṣapas
= π/6 cubic sarṣapas
Now, volume of right circular cylinder
= π x (radius)2 x height................. (1)
Now, we should know the height of the right circular conical heap above the cylinder.[2] According to the Tilokasāra,[3] if the seeds of tila, sarṣapa, valla, arhada, caṇā (gram), atasi, kulattha, rajāmaṣa etc. are filled in a right circular cylinder in such a way that a conical heap is formed, then
height of the conical heap = circumfernce of the circular base of the cylinder /11
Volume of the right circular cone
= 1/3 π (radius)2 x height
[4] = [1/3 π (radius)2] x
= 1/3 π (radius)2 x
= 2/33 π2 (radius)3........................................ (2)
Now, putting the values of radius and height in equation no. 1 above, we get the
Volume of right circular cylinder
= π x (12288 x 1011)2 x (24576 x 109) cubic-sarṣapasVolume of one seed of sarṣapa is π/6 cubic sarṣapas. Therefore, the number of sarṣapa seeds in the cylinder
= 6 x (12288 x 1011)2 x (24576 x 109)
= 222,651,104,624,64 x 1031
= 2.226 x 1044 approximately................... (3)
By substituting the value of radius in equation no. 2, we get the volume of right circular conical heap
= 12/33 x π x (12288 x 1011)3
= 2.119 x 1045 approximately[5]................... (4)
The number of sarṣapas in the conical heap
= 2.341 x 1045 approximately.[6]
Thus, the total number of seeds in the cylinderical container of 10000 yojanas diameter and 1000 yojanas height together with the conical heap is 2.341 x 1045.
We have seen that
(1) Volume of the cylindrical container is
= πr2h
where r is the radius of the circular base and h is the height of the cylinder
(2) Volume of the conical heap is
= 2/33 π2r2
(radius of the circular base of the cone is also r).
(3) Volume of a single seed is π/6
Thus, the total number of seeds in the cylindrical container with the conical heap above is
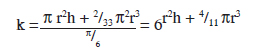
Now we know that h, the height of the cylindrical container, is the same in all containers A, B, C and Xo, X1, X2...... etc. but the r, the radius is different in them.
Value of h is
= 24576 x 109 sarṣapa
The anavasthita cylinders are made again and again with changed diameters. Let us denote
the original anavasthita cylinder as Xo
firstly made new anavasthita cylinder as X1
secondly made new anavasthita cylinder as X2
and so on.
Let the
radius of Xo be denoted as ro
radius of X1 be denoted as r1
radius of X2 be denoted as r2
and so on.
Radius of A, B and C is also ro, which is
= 12288 x 1011 sarṣapas.
Let ko, k1, k2...... denote the total number of seeds in Xo, X1,X2...... respectively.
Thus,
ko = 6ro2h + 4/11 πro3 .................. (0)
= 2.341 x 1045 approximately.
Now, by dropping one seed each from Xo into the rings of continents and oceans, the last seed will be dropped in the ko th ring with radius
r1, = 2(ko-1)ro = 2(ko-2) x 2ro
Now, as 2ro = 1 lakh yojanas
r1 = 2(ko-2) lakh yojanas
When Xo becomes emptied, one seed is dropped in the cylinder A.
Total number of seeds contained in X1 is
X1 = 6r12h + 4/11 πr13.................. (1)
[7] = 6 [22(ko-1)ro2]h + 4/11 π[23(ko-1)ro3]
Now, by dropping one seed each in the rings ahead the last seed will be dropped in
(ko+k1)th ring.
The radius of this ring will be
r2 = 2(ko+k1-2) lakh yojanas
= 2(ko+k1-1)ro
In this way, on emptying the X1, second seed will be dropped in the cylinder A.
Total number of seeds in X2 will be
k2 = 6r2 2 h + 4/11 πr23.................. (2)
In the above manner, the last seed of X2 will be dropped in (ko+k1+k2)th ring.
Now, third seed will be dropped in the cylinder A and X3 will be made with radius r3.
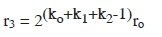
Total number of seeds in X3 will be
k3 = 6r32h + 4/11 πr3 3.................. (3)
This process will continue till A is filled completely with a conical heap above. It means that when ko seeds will be dropped in A, it will be so filled. This will happen when the cylinder
Xko-1 will be emptied. Its last seed will be dropped in the
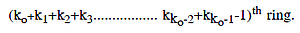
Now the first seed will be dropped in the cylinder B, and a new anavasthita cylinder Xko will be made. Its radius will be

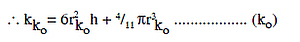
Now, again to fill the cylinder A which is already emptied, the whole process as above will be repeated. It means that when the cylinder X2ko-1 will be emptied, cylinder A will be filled second time and then the second seed will be dropped in the cylinder B. Thus, by repeating the above process ko times, the cylinder B will be completely filled. This will happen when the cylinder X2k0-1 will be emptied. Its last seed will be dropped in the
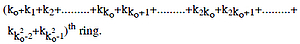
Now the first seed will be dropped in the cylinder C, and a new anavasthita cylinder 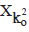 will be made. Its radius will be
will be made. Its radius will be 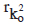 and the total number of seeds contained in it will be
and the total number of seeds contained in it will be 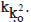 The values of
The values of 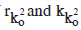 can be found from the original equations.
can be found from the original equations.
Now, by repeating the process again ko times, the cylinder C will be completely filled. This will happen when the cylinder 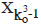 will be emptied. Its last seed will be dropped in the
will be emptied. Its last seed will be dropped in the
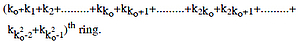
Now all the three cylinders A, B and C are completely filled. A new anavasthita cylinder 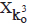 will be made. The radius
will be made. The radius 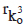 will be given by
will be given by
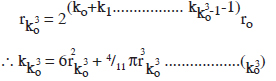
The number Utkṛṣṭa Saṃkhyāta (U. S.)
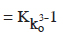
Now, we can see that although the value of kko 3 is definitely defined by the equation (o) to K02, yet it will not be possible to compute it mathematically in terms of digits. However, by substituting approximate values of ko etc. in the above equations, we can get a glimpse of the gigentic value of U. S.
By simplifying the equations (1) to (kko 2) as shown in foot note no. 1 on p. 362, and by neglecting the second term therein, we get
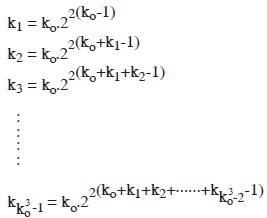
And 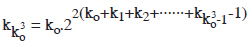
Now, by putting the values of k1, k2 in these equations, we get,
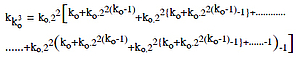
By putting k′ in place of ko-1 of and expanding the right side of equation we get
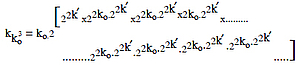
Now, the value of the last term of the right side is the highest and values of other terms are not less than one; hence, by neglecting other terms, we get,
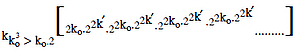
By substituting
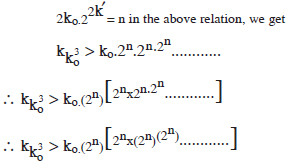
Now by putting m in place of 2n in the above relation we get,
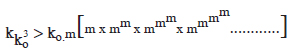
Now, the last term in the above relation will have the highest value. It will be
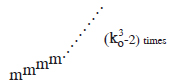
Thus, by neglecting other terms, we get
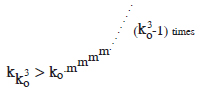
here m = 2n and
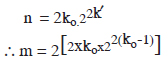
We have already found out that ko>1045. By using logarithm,[8] we get,
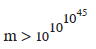
Thus the value of 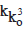 is greater than
is greater than
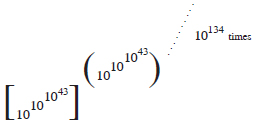
It means that the value of 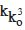 is greater than the number obtained by raising
is greater than the number obtained by raising
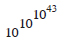
to itself 10133 times.[9]
Trilokasāra with the bhāṣā-ṭikā (commentary in vernacular language) by Pt. Todarmalji, śloka 18. However, in the Lalitavistara of Buddhist tradition, we get:
7 sarṣapas = 1 yava
7 yavas = 1 aṅgulī-parva.
Dr. Laxmichand Jain, in his Prastāvanā (Preface) to 'Jambūdvīpapṇṇattisaṃgaho', has written an essay titled 'Tiloyapaṇṇatti kā Gaṇita' (mathematics of Tilloyapaṇṇattī), in which he writes: "Here, we do not know how much and why this height of the cone is taken."
Tilasarisavavallāḍhai caṇaatasikulattharāyamāsādi pariṇāhekkārasamo vaho jadi gayaṇgo rāsī-Trilokasāra, vese 23
volume = 1/3 π (radius)2
= 1/3 x 3 x (radius)2
= (radius)2
And also {{46ee6124bc36f9fa54d7f388c89c54e2722776f1}}= (radius)2
That is, 1/3 π (radius)2 = (circumference/6)2 But, as we have already seen the correct value of π is not 3, but 3.1415..... (See, Appendix II, supra p. 346).This value is found with the help of logarithm. The value of log π is taken as.4971. If we want to get the exact value of the number of seeds of sarṣapa contained in the conical heap, we have to take the value of π up to 32 decimal points. Here, however, we have taken this value up to 4 decimal points.
1. Value of π is taken as 3.
2. The volume of the sphere is taken as 9/2 (radius)3.
3. The volume of the right circular cone of the height Oce/11 is
{{c924d6fcbde8f5b76dfc6d0f91e11956b11f312c}}
4. Volume of cylinderical container is taken as [3 x (radius)2 x (height)]
The value thus found would be only approximately correct. In Trilokasāra, this value (of the no. of seeds in the cylindrical container) is given to be 197,912,092,999,680,000,000,000,000,000,000,000,000,000,000 and no. of seeds in the conical heap is given as 179, 920, 084, 545, 163, 636, 363, 636, 363, 636, 363, 636, 363, 636, 363, 336, 64/11. Total no. of seeds required is given as 199, 711, 293, 845, 131, 636, 363, 636, 363, 636, 363, 636, 363, 636, 363, 636, 363, 64/11 = 1.997 x 1045 approximately Prof. Muni Mahendra Kumar
Prof. Muni Mahendra Kumar