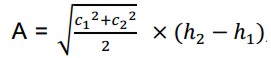SOAS Centre for Jaina Studies
18th Jaina Studies Symposium
Jainism and ScienceBook of Abstracts
19 March 2016
SOAS, University of LondonUpakāra in Akalaṅka's Tattvārthavārtika
Jaina versus Brahmanical MathematiciansAna Bajželj, Postdoctoral Polonsky Academy, The Van Leer Jerusalem Institute, Israel
In the sūtras 5.17–22 of his Tattvārthasūtra Umāsvāti lists various kinds of assistance (upakāra) in the production of certain effects that the six basic types of substances provide. Dharma and adharma respectively support motion and rest, ākāśa acts as a receptacle, pudgalas support the body, speech, mind, breath, pleasure, pain, life and death, jīvas support one another and kāla assists continuity, transformation, activity and posteriority and priority. In his commentary to the sūtras Akalaṅka explains each case of assistance in detail, elucidating the relation between substances, their assisting functions and the effects the production of which they assist. He emphasises that the assisting function of each particular type of substance cannot be performed by any factor other than itself. Furthermore, substances can never lose the inherent capacity to assist in their specific ways even in the absence of recipients of their assistance. The assisting functions of substances are, then, significant aspects of the metaphysics at hand. They are essentially involved in the causal relations that bring about some of the most elementary worldly phenomena. As such they are vital factors to consider when researching the Jain doctrine of causality that was developed as a part of a greater
Jain “scientific” endeavour to systematically and rationally explain the nature of reality.
Despite that upakāras have received only scarce scholarly attention. Secondary sources mostly refer to them in terms of substances functioning as auxiliary causes of particular effects but aside from comparing them to specific auxiliary causes like water, earth, shade of a tree, potter‟s wheel etc. they do not go into much detail in their descriptions of them. This paper will examine Akalaṅka‟s account of the different kinds of upakāras, discerning their distinguishing characteristics and analysing the causal dynamics that are involved in their operation. Since Akalaṅka‟s Tattvārthavārtika was influenced by Pūjyapāda‟s Sarvārthasiddhi, it will be read against the latter in order to note which of Akalaṅka‟s explanations and arguments with regard to the different upakāras reiterated the words of his predecessor and which were novel in the Digambara Tattvārthasūtra commentarial enterprise.
When Science Meets Fiction: On Technical Passages in Jain Medieval NovelsJohannes Bronkhorst, University of Lausanne, Switzerland,
Unlike the Buddhists, Jaina authors have contributed in an important manner to the history of mathematics in India. Unfortunately many of their texts have not survived, but what has survived allows us to form a good impression.
The present paper concentrates on the way in which Jaina and Brahmanical mathematicians related to each other. About this there is very little explicit evidence, but a passage in Bhāskara‟s (Bhāskara I) Āryabhaṭīya-bhāṣya (7th century CE) provides interesting information. Bhāskara here criticizes(though implicitly) a Jaina mathematician by showing that the latter‟s theorem has unacceptable results. This can be contrasted with Bhāskara‟s uncritical attitude toward Āryabhaṭa, the inspired teacher of his own school. The conclusion to be drawn is that mathematics in India never cultivated the critical attitude that characterizes much of Indian philosophy. In mathematics it appears that criticism was exclusively directed at authors and texts belonging to different traditions than one‟s own.
Christine Chojnacki, University Lyon 3, FranceJain Literature is mostly renowned for its canonical texts and vast amount of treasures of stories. However, sciences have not been neglected either by writers of this community. On the one hand, several authors from the classical period (for instance Āryabhāṭa) or from the medieval period (thus Thakkura Pheru) have composed treatises on technical topics. On the other hand, besides these systematic treatments of scientific knowledge, one can find in Jain novels written from the 8th to the 12th century various passages inspired from different kinds of śāstras (jyotiḥśāstra, ayurveda, aśvaśāstra, lakṣaṇaśāstra, nimittaśāstra). The purpose of this article will be to investigate several ofthese passages. We will discuss what they can teach in comparison to other sources of their times and see what they can add for the chronology of the extant material at our disposal.
Jainism and Science: History and Ontology of the ‘Soul’
Peter Flügel, SOAS
The paper discusses attempts by modern scientists to reconstruct and theoretically explain the historical origins of conceptions of „soul‟ or „self‟ across cultures in the light of ancient Indian debates on the Jaina approach of positing the individual jīva or ātman as an eternal substance and speculates on the functions of dualist ontological commitments.
Scientific Knowledge in Jainism
Marie-Hélène Gorisse, SOAS & Ghent University, Belgium
This lecture is intended as an investigation upon the nature, place and function of scientific knowledge in Jainism. First of all, how and what can we know according to the Jaina religious soteriological perspective? Does the concept of a complex knowable involve a plurality of types of knowables? And is there a cognizer-independent (theory-free) reality that the soul, respectively the mind, can cognize? An innovative way of tackling this last issue is found in the classification of sources of reliable knowledge (pramāṇa) offered by Jaina philosophers, when they seek the criterion that will produce a clear distinction between direct and indirect sources of reliable knowledge. Akalaṅka‟s treatises (720-780), especially the Laghīyastraya, are precious for such considerations since, at the time of his attempt to offer a Jaina theory of knowledge recognizable as such, Akalaṅka was committed to three different agendas on this issue, namely the Buddhist agenda of distinguishing between conceptual and non-conceptual knowledge; the chronologically descriptive agenda of distinguishing between simple and complex knowledge; as well as the Jaina agenda of distinguishing between knowledge mediated or not mediated by the mind and the senses. At this step, I will advance an interpretation concerning the types of knowledge that are following the scientific method in this classification.
The second part of the lecture will be to draw the consequences of this conception on chosen epistemological issues. First, if scientific empirical knowledge is theory-dependent, in which sense is it reliable? And what does ultimately found, as well as what does account for, its reliability? Is it extra-mundane types of knowledge, is it the consensus of a community, or is it another instance of validation? What is more, if a God-eye‟s view with a non-communicable content exists, does falsifiability only concern the linguistic (infinite number of) interpretations of this view? Finally, Jainism offers an original treatment of the links between logic and proof in science, since logic is conceived in terms of interaction between agents and is more adapted to empirical situations.
Newly Discovered Jaina Mathematical Manuscripts and their Content
Anupam Jain, Government Degree College, Sanwer, Indore, India
Mathematics is an integral part of Jaina literature because it is used as a tool to explain:
- Cosmological data & description of the three-fold universe. It is used in giving the length, area and volume of the different sections of the universe and dimensions of mountains, rivers and parts of Jambūdvīpa.
- Different types and sub-types of karmas, the operations of uprising, binding and shedding of karmas and the net effect of their infinitude of combinations on living beings.
- Jaina logic system, which is used for establishment of logical facts and reconcilement of the others‟ views. Modern mathematical logic is available in the texts of Jaina Nyāya (Logic).
It is also used:
- To determine auspicious places & times for religious ceremonies like dīkṣā (initiation) & pratiṣṭhā (consecration).
- To train pupils (householders) in basic Mathematics (Laukika Gaņita) required in daily life.
Due to so much importance of Mathematics in Jainism, Jaina scholars wrote complete mathematical texts. Many of them are still not known to the academic world. We have made an extensive survey of different old Jaina libraries and discovered many completely mathematical (including astronomical) texts or religious texts full of mathematical knowledge:
- Jyotirjñānavidhi of Śrīdharācārya [799 C.E.]
- Gaṇitasāra of Śrīdharācārya [799 C.E.]
- Ṣaṭatrinśikā or Ṣaṭatrinśatikā of Mādhavacandra Trividya [11th c.C.E.
- Commentary on Gaṇitasārasaṃgraha of Mahāvīrācārya by Bhaṭṭāraka Sumatikriti [16th c.C.E.]
- Iṣṭāṅkapañcaviṃśatikā of Tejasiṃha [1646–1686 C.E.]
- Gaṇitasāra of Hemarāja [1673 C.E.
Three more manuscripts which are related to Cosmography / Cosmology and having a lot of material of mathematicians‟ interest are the following:
- Lokānuyoga by Jinasena I [783 C.E.]
- Trailokyadīpaka of Pt. Vāmadeva [14th c.C.E.
- Trilokadarpaṇa of Kavi Khadagasena [1656 C.E.
Detailed information about the source, no. of copies, periods and content of these manuscripts will be presented in the lecture.
Space and Time: In the Perspectives of Jainism and Science
Rajmal Jain, Kadi Sarva Vishvavidyalay, Ahmedabad & Anupam Jain, Indore
We will briefly describe philosophy and concepts of the space and time in Jainism and modern science. Important milestones / discoveries over time will be described. Though Jainism has fundamental differences with science regarding the formation of the universe, it has well defined concepts of space and time with quantitative descriptions. Considering this unique opportunity we investigate in greater detail the units of space and time in Jainism and compare them with those of currently advanced sciences. We present complete descriptions of sub-units of time from samaya to muhūrta and their quantitative conversion to seconds / minutes of present time. Further, the niścaya-kāla and vyavahāra-kāla defined in Jaina canonical texts have been described scientifically basedon mass, momentum and energy conservation laws, and we propose a mathematical function for the vyavahāra-kāla. We present measurements of smallest length/ distance parmāṇu to largest: yojana / rajju, and show their relationship with current modern units of distances. We review features of Jainastronomy in contrast to modern astronomy and present estimates of distances for the planets and other celestial bodies in the solar system described in Jainism and compare the units with that mentioned in modern astronomy.
Architectural Science in Jain Poetry: Descriptions of Kumārapāla’s Temples
Basile Leclère, Université de Lyon 3, France
After his conversion to Jain faith due to the influence of the famous Śvetāmbara monk Hemacandra, the Caulukya king Kumārapāla (r. 1143-1173) ordered Jain sanctuaries to be erected throughout his dominion. This ambitious monumental program was duly praised by Hemacandra in the concluding section of the Triṣaṣṭiśalākāpuruṣa-caritra. Indeed, in that work, he made Mahāvīra himself predict that Kumārapāla, “with unlimited power, will make this earth adorned with temples of the Jinas in almost every village” (translation Helen Johnson). Many other Jain writers from the twelfth and thirteenth centuries extolled Kumārapāla as a great builder, and some of them, in order to insist on his lavish patronage, even described in detail the most impressive temples set up on his order, beginning with the great religious complexes of the capital city Aṇahillapātaka. In the present paper, I intend to demonstrate that, if these authors may have been influenced by poetical conventions, their descriptions are nonetheless pervaded by technical terms which betray a genuine knowledge of architecture among Jain scholars. Given that very few Jain temples from the reign of Kumārapāla have survived through the centuries, these textual data could be fruitfully explored in order to complete the information provided by temple inscriptions and architectural treatises.
The Enigma of Cosmogony
Muni Mahendra Kumar, Jain Vishva Bharati Institute, Ladnun, India
According to the Jain canonical texts, the universe (the cosmos) is beginningless with respect to time. In modern scientific cosmogony, there are several hypotheses which are divided on the issue of the beginning of the Universe. In the present paper, a brief review of the different models presented by the astronomists is made and critically examined on the basis of scientific aspects as well as logical ones. The most popular view in the modern times is the “big bang theory”. Although most scientists are in favour of this model, it is not unanimously accepted. The main alternative articulated by Fred
Hoyle, Hermann Bondy and Thomas Gold is the theory of the “steady state universe”. The Indian scientist J.V Narlikar together with Fred Hoyle has, on the basis of the hypothesis of new creation of matter, refuted the big bang theory and supported the steady state theory. More recently, another Indian scientist, Saurya Das, who has now settled in the U.S.A., has worked out the mathematical equations giving solution to the age of universe. He is also of the view that the universe is ultimately eternal - without a beginning and without an end. This view seems to be very similar to the Jain view. The paper will draw the logical conclusion in the favour of the Jain view. The main scientific evidence for the big bang theory, viz., red shift, which shows the expansion of space, has been critically examined, and finally shown to be only hypothetical, and hence, cannot be considered as a truly scientifically valid concept.
Siṃhatilakasūri’s Mathematical Commentary (13th c. CE) on the Gaṇitatilaka
Alessandra Petrocchi, University of Cambridge, UK
My paper presents the Sanskrit mathematical text written by Siṃhatilakasūri (13th c. CE),
which is a commentary on Śrīpati‟s Gaṇitatilaka (11th c. CE). Siṃhatilakasūri‟s work has come down to us in a uniquely extant yet incomplete manuscript published by Kāpadīā in 1937. Siṃhatilaka‟s commentary is a precious source of information on early medieval mathematical practices. This is in fact the first Sanskrit commentary fully dedicated to Indian mathematics and the first written by a Jaina that seems to have survived to the present day. This text has never been studied or translated into English.
Siṃhatilakasūri (13th c. CE) was a Śvetāmbara Jaina monk of the Kharatara-gaccha from thirteenth century Gujarat. His writings also include a Sanskrit commentary on the popular Bhuvanadīpaka, a treatise by Padmaprabhasūri on the branch of astrology called praśna or “interrogations” and five Sanskrit works on Jaina mantras and rituals. His Mantrarājarahasya is the first and one of the few Jaina ritual handbooks on the sūrimantra that have come down to us.
In my paper, I shall address the following key-questions: How does the commentator explain mathematical rules while expanding Śrīpati‟s concise style? What is the terminology used and how does this differ from other mathematical commentaries? What one can say about the relationship between the linguistic formulas and mathematical objects found in the commentary? For this reason, I shall investigate Siṃhatilaka‟s presentation of mathematical rules and sample problems on the operation of addition of integers, on barter and exchange, and on the class of fractions of the root-remainder.
Jain Theory of Timelessness
Samani Unnata Pragya (SOAS, Jain Vishva Bharat Institute Ladnun)
Time denotes „now-ness‟, and „is-ness‟, is also a measure of change. This paper will analyse the „timelessness theory‟ / „zero time theory‟ (I use both words interchangeably with same meaning) as found in the Jain literature and philosophy. The mention of zero time to render a conceptual meaning in Bhagavaī and the absence of zero time in the „time chart‟ of Anuyogadārāiṃ is worth analysis. The research will reflect possibility of different kinds of „timelessness‟ based on anekāntic philosophy.
Those are immeasurable time as „timeless‟, beyond time as „timeless‟ and existence without time as „timeless‟. Further the paper will discuss the source of these different kinds being different subject areas: „immeasurable‟ timelessness is merely epistemological as found in aspṛśada gati, „beyond time‟ is metaphysical in origin, where a case like artha-paryāya cannot be measured, and „existence without time‟ is cosmological, since supra cosmos lacks time.
Jinabhadragaṇi Kṣamāśramaṇa: Computational Wizard of Sixth Century C.E.
Ratnakumar Shah, Pune, India
Some scholars think that alphabetical and numeric symbols including zero with place value started with Āryabhaṭa I (496 A.D.) as reported by Bhāskara I. [1; p. 168]. In this article an attempt is made to show that Jinabhadragaṇi Kṣamāśramaṇa (JB), a great Jaina saint-scholar who was almost a contemporary of Āryabhaṭa I, had almost employed modern methods of arithmetical processes in decimal system with zero having place value, showing great proficiency in dealing with addition, subtraction, multiplication, division, extraction of square roots, operations with fractions, mensuration of triangle, trapezium, circle etc. and use of rule of three. Although his works Bṛhatkṣetrasamāsa (BK) [2], Bṛhatsangrahaṇi (BS) [3], and Viśeṣāvaśyakabhāṣya (VB) [4] are all in poetic form where all numbers are expressed in words and no symbols for numerals appear therein, yet the processes described, numbers uttered digit-wise and calculations involving very large numbers leave not an iota of doubt that some symbol of zero was existing then and the system of manual calculations existing then was same as employed at present. While extracting square roots such large numbers were tackled by JB with such ease and precision, and the numbers uttered in word-form (including zero as suṇṇa) clearly show that the decimal system with zero having place value must be in vogue at least for a couple of centuries. His formula for area between 2 parallel chords of a circle, viz.
where c1 and c2 are the lengths of chords and h1 and h2 are the heights of segments subtended by them, gives a very high degree of approximation. His method of calculation of the area of the Lavaṇa Sea (= 99 611 715 000 square yojanas) and its volume (- 1 693 399 155 000 000 cubic yojanas) reminds us of pre-calculus method of indivisibles adopted by Cavelieri and Roberval in 17thC. A.D.
The Treatment of Series in the Gaṇitasārasaṃgraha of Mahāvīrācārya and its Connections to Jaina Cosmology
Cathérine Morice-Singh (Université Sorbonne Nouvelle - Paris 3)
It is well known that, in his Gaṇitasārasaṃgraha (GSS), Mahāvīrācārya teaches the addition and subtraction of series instead of ordinary addition and subtraction of numbers. He places these two fundamental operations in a logical manner at the end of his chapter on operations (parikarman) as they anticipate the knowledge of the other operations like multiplication, division, square and square-root, etc. The presentation discusses his treatment of arithmetical as well as geometrical series, which occupies nearly half of the chapter itself, and argue that these series are given a special place because they play a great role in Jaina cosmology. Cases will be presented in support of this view.