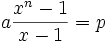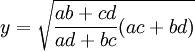Lifetime
Born: ~800 CEPassed away: ~870 CE
About
Mahāvīrācāryawas a 9th-century Indian Jain mathematician from Gulbarga who asserted that the square root of a negative number did not exist. He gave the sum of a series whose terms are squares of an arithmetical progression and empirical rules for area and perimeter of an ellipse. He was patronised by the great Rashtrakuta king Amoghavarsha.
Mahavira was the author of Ganit Saar Sangraha. He separated Astrology from Mathematics. He expounded on the same subjects on which Aryabhata and Brahmagupta contended, but he expressed them more clearly. He is highly respected among Indian Mathematicians, because of his establishment of terminology for concepts such as equilateral, and isosceles triangle; rhombus; circle and semicircle. Mahavira's eminence spread in all South India and his books proved inspirational to other Mathematicians in Southern India.[2] It was translated into Telugu language by Pavuluri Mallana as Saar Sangraha Ganitam.
Higher-order equations
Mahavira solved higher order equations of n degree of the forms:
and
Formula for cyclic quadrilateral
Aditya expressed characteristics of a cyclic quadrilateral, like Brahmagupta did previously. He also established equations for the sides and diagonal of Cyclic Quadrilateral.
If sides of Cyclic Quadrilateral are a, b, c, d and its diagonals are x and y while
And
Then,