Dimensions in whole numbers are called integer.
Fractal numbers also play a role in dimensions and will be introduced later.
Dimensions in mathematical language:
point D 0 0-dimensional line D 1 1-dimensional plane D 2 2-dimensional space D 3 3-dimensional etc... in general D n n-dimensional The mathematical view is an abstract view - there is no limit in numbers of dimensions.
- Dimensions are defined as degrees of freedom in movements.
dimensionality: degrees of freedom in movements
5 Dimensions
| 0 | 1 | 2 | 3 | 4 |
Now we have descriptions of dimensions in 3 languages:
| Language | Dimensions | ||||
| numerical | 0 | 1 | 2 | 3 | 4 |
| mathematical | D 0 | D 1 | D 2 | D 3 | D 4 |
| geometrical | Point -?- | Line | Plane | Space | no name -?- |
Zero dimension and 4th dimension are added to the scheme.
Brief History of Ideas on Dimensionality.
- Euclid:
In the formulation of Euclidean geometry a fourth dimension was not even considered.
- Aristotle:
He was the first person to state categorically that the fourth dimension is impossible. In his work 'On Heaven' he wrote, "The line has magnitude in one way, the plane in two ways, and the solid in three ways, and beyond these there is no other magnitude because the three are all."
- Ptolemy: (A.D.150)
In his book 'On Distance' Ptolemy gave a 'proof' that the fourth dimension is impossible. Draw three mutually perpendicular lines he suggested. Try to draw another line perpendicular to all of these lines. It is impossible. The fourth perpendicular line is "entirely without measure and without definition." The fourth dimension is impossible.
This is really not a legitimate proof of the 4th dimension. It is merely a proof that we cannot visualize the 4th dimension.
- Riemann:
On June 10, 1854 a new way of looking at geometry was put forward in a famous lecture by the mathematician Bernhard Riemann. He generalized Euclidean geometry to a non-Euclidean geometry allowing for curved surfaces and any number of higher dimensions.
To find out more about the 4th dimension, let's have a closer look to corresponding geometrical objects.
Lets Go Hyperspace
To be well prepared, use mathworld links in the last right column
- mathworld.wolfram.com links supplies nice visualisations - really great for understanding.
- You can e.g. touch a cube with your PC mouse and turn it in all possible directions... and a lot more... strongly recomended to try out.
| dimension | geometrical | objects | mathworld links |
| 0 | point |  | point |
| 1 | line | 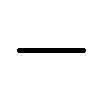 | line |
| 2 | plane |  | square, rectangle |
| 3 | space | 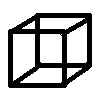 | cube |
| 4 | hyperspace | 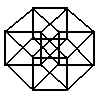 | tesseract |
Projections:
PC screen is 2-dimensional, a plane delivering a picture.
The picture of a cube on screen is the projection of a real (3D) cube on 2D.
For a cube many different projections are possible.
Mostly, our eyes recognize them immediately as a 3D cube object.
The other way round:
- The picture of a cube (2D) represents a real cube (3D)
To enter geometricalhyperspace (4th dimension), we use a simple geometrical construction law:
Abstract:
-
- Drop a perpendicular on the point to get a line.
- Drop a perpendicular on the line to get a rectangle(square).
- Drop a perpendicular on the square to get a cube.
- Drop a perpendicular on the cube to get a tesseract. (Oops no headache please)
Visualized: "move perpendicular"
| dimension | geometrical | perpendicular | move |
| 0 | point |  | point |
| 1 | line | 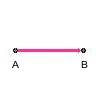 | line: |
| 2 | plane | 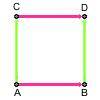 | square: |
| 3 | space | 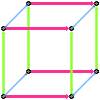 | cube: |
| 4 | hyperspace | 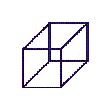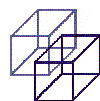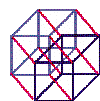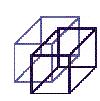 |
- Move Point A along the red line perpendicular to point B to get a line.
- Move red line (A-B) perpendicular (along the green line) to position C-D to get a square (ABCD)
- Move the square (ABCD) perpendicular (along the light blue line) to get a cube.
- .... don't move - just have a look at the animation of a tesseract building scheme.
Our imagination simply quits when we try to move a cube "perpenticular" to it's base, the space, in real.
But we can "construct" a 4D tesseract object by this law of moving perpendicular.
The above construction view of a tesseract is one of many possible projections of a tesseract.
[ projection of 4D onto 3D onto 2D ]
Next chapter shows a tesseract in motion (4D).
 Editor Aparigraha Jain
Editor Aparigraha Jain
 Editor Carla Geerdes
Editor Carla Geerdes

