Dimensional Views [ 01.08 ] Special : Moebius Strip and Tesseract

Let's build our own moebius strip:

Take a strip of paper: L ength ~ 30 cm, width ~ 4 cm

Give it a half twist

Tape the ends together

Now we are ready to find out what a nonorientable surface is:

• When you take the strip of paper between thumb and first finger - you are sure you touch the 2 sides of the strip.

Now let's proof the moebius strip has only 1 side:

• Take a pen and draw a line along the middle of the strip marking the surface:

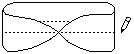
You end on the same side as you started.

That means:

1. Back and front are the same = there is only 1 side.
2. There is only 1 border (although you can touch and see 2).

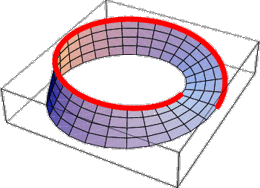Start marking one border with a coloured pen.... you end up where you started on the same border - after 2 rounds.

Moebius Strip Inside the Tesseract

Now we put one of the 8 cubes of the tesseract on our moebius strip:

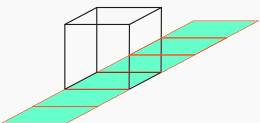...and move it along the surface....after the 1st round.... on the same position: bottom is on top!

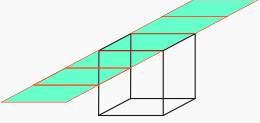The 8 cubes of a tesseract are moving simultanously on moebius strips in 4D hyperspace, which is hard to imagine. The single cube on a moebius strip proves that it is possible: top = bottom and viceversa while moving on a nonorientable surface.

• Remember, we draw a line along the middle of the strip marking the surface:
  

• Not 2 stripes by cutting (as exspected)
• but doubled the length of the moebius strip!